Nous allons réaliser un programme Julia pour résoudre numériquement et visualiser l’équation d’un cercle. Plus précisément, notre objectif est de :
- Résoudre l’équation (x-1)² + (y-2)² - 1 = 0, qui représente un cercle de rayon 1 centré en (1, 2).
- Visualiser la grille de recherche, les solutions trouvées et le cercle théorique.
- Vérifier la précision de nos résultats en calculant la distance entre chaque solution et le centre du cercle.
Notre programme utilisera une approche par force brute, en évaluant l’équation sur une grille de points dans un espace bidimensionnel. Nous afficherons ensuite les résultats graphiquement et numériquement pour une analyse approfondie.
using Plots
function f(x, y)
return (x - 1)^2 + (y - 2)^2 - 1
end
function solve_equation(x_range, y_range, tolerance)
solutions = Tuple{Float64, Float64}[]
grid_points = Tuple{Float64, Float64}[]
for x in x_range
for y in y_range
push!(grid_points, (x, y))
abs(f(x, y)) < tolerance && push!(solutions, (x, y))
end
end
return solutions, grid_points
end
function plot_results(solutions, grid_points)
p = plot(aspect_ratio=:equal, xlabel="x", ylabel="y",
title="Solutions of (x-1)² + (y-2)² - 1 = 0",
xlims=(-10, 10), ylims=(-10, 10))
scatter!(p, grid_points, label="Grid Points", color=:lightgray,
markersize=1, markerstrokewidth=0, alpha=0.5)
t = 0:0.01:2π
plot!(p, cos.(t) .+ 1, sin.(t) .+ 2, label="Theoretical Circle",
color=:black, linewidth=2)
scatter!(p, solutions, label="Numerical Solutions",
color=:red, markersize=3)
scatter!(p, [1], [2], label="Center (1, 2)", color=:blue, markersize=5)
hline!(p, [0], color=:gray, label="x-axis", linewidth=1)
vline!(p, [0], color=:gray, label="y-axis", linewidth=1)
display(p)
end
function print_results(solutions, grid_points)
println("Total number of grid points: $(length(grid_points))")
println("Total number of solutions: $(length(solutions))")
println("\nSome solutions found:")
for (i, (x, y)) in enumerate(solutions)
if i <= 5
println("x = $x, y = $y")
elseif i == 6
println("...")
break
end
end
println("\nChecking distances from center (1, 2):")
for (i, (x, y)) in enumerate(solutions)
if i <= 5
distance = sqrt((x - 1)^2 + (y - 2)^2)
println("Solution ($x, $y): distance = $distance")
elseif i == 6
println("...")
break
end
end
end
x_range = y_range = -10:0.1:10
tolerance = 0.01
solutions, grid_points = solve_equation(x_range, y_range, tolerance)
plot_results(solutions, grid_points)
print_results(solutions, grid_points)Maintenant, examinons en détail comment ce code fonctionne pour atteindre nos objectifs :
- Nous commençons par importer la bibliothèque Plots, essentielle pour la visualisation de nos résultats.
- La fonction
f(x, y)définit l’équation de notre cercle. Elle retourne la valeur de (x-1)² + (y-2)² - 1 pour chaque point (x, y). - La fonction
solve_equationest le cœur de notre résolution numérique :- Elle parcourt une grille de points définie par x_range et y_range.
- Chaque point de la grille est stocké pour la visualisation ultérieure.
- Si la valeur absolue de f(x,y) est inférieure à notre tolérance, le point est considéré comme une solution.
- La fonction
plot_resultscrée une visualisation complète de nos résultats :- Elle affiche tous les points de la grille en gris clair, donnant un aperçu de notre espace de recherche.
- Le cercle théorique est tracé en noir pour comparaison.
- Les solutions numériques sont marquées en rouge, permettant de voir leur distribution autour du cercle théorique.
- Le centre du cercle (1, 2) est mis en évidence en bleu.
- Les axes x et y sont ajoutés pour une meilleure orientation.
- La fonction
print_resultsfournit une analyse numérique de nos résultats :- Elle affiche le nombre total de points de la grille examinés.
- Elle affiche le nombre total de solutions trouvées.
- Elle liste les cinq premières solutions pour un aperçu rapide.
- Pour chaque solution, elle calcule et affiche la distance par rapport au centre du cercle, permettant de vérifier la précision de nos résultats.
- Dans la partie principale du script, nous définissons nos paramètres :
- Les plages x et y vont de -10 à 10 avec un pas de 0.1, offrant une vue étendue autour du cercle.
- La tolérance est fixée à 0.01, déterminant la précision de nos solutions.
- Enfin, nous exécutons notre processus de résolution, affichons les résultats graphiquement, et imprimons les analyses numériques.
Ce programme nous permet non seulement de résoudre numériquement l’équation du cercle, mais aussi de visualiser le processus de résolution et de vérifier la précision de nos résultats. C’est un excellent outil pour comprendre la relation entre les équations algébriques et leur représentation géométrique, ainsi que pour explorer les méthodes de résolution numérique.
L’exécution de ce programme affiche dans la console ceci :
Total number of grid points: 40401
Total number of solutions: 12
Some solutions found:
x = 0.0, y = 2.0
x = 0.2, y = 1.4
x = 0.2, y = 2.6
x = 0.4, y = 1.2
x = 0.4, y = 2.8
...
Checking distances from center (1, 2):
Solution (0.0, 2.0): distance = 1.0
Solution (0.2, 1.4): distance = 1.0
Solution (0.2, 2.6): distance = 1.0
Solution (0.4, 1.2): distance = 1.0
Solution (0.4, 2.8): distance = 0.9999999999999998
...
et le graphique suivant est obtenu
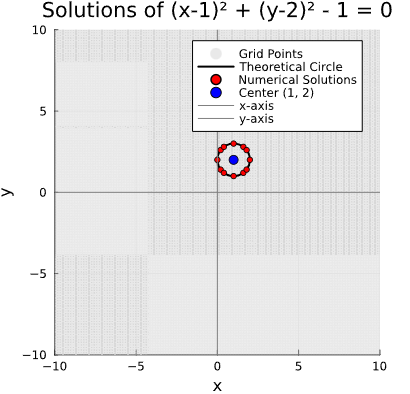
40401 représente le nombre total de points évalués dans notre recherche de solutions. Il est calculé comme le produit du nombre de points dans la plage x et dans la plage y (201 * 201 = 40401, car nous avons 201 points de -10 à 10 avec un pas de 0.1).
Le programme détecte, avec la tolérance fixée, 12 points solutions de l’équation.
Performance monothread
Nous allons désormais faire quelques mesures de performance du “cœur” de ce code.
Nous utiliserons les outils de profilage de Julia, notamment la macro @time pour des mesures simples, et le package BenchmarkTools pour des mesures plus précises et répétées.
Afin d’utiliser BenchmarkTools dans Julia, il faut d’abord l’installer. BenchmarkTools est un package externe qui n’est pas inclus dans l’installation standard de Julia. Voici comment procéder pour l’installer :
-
Ouvrez une session Julia (soit dans le terminal, soit dans un environnement de développement intégré comme VS Code avec l’extension Julia).
-
Entrez dans le mode gestionnaire de paquets en appuyant sur
](crochet fermant). -
Dans ce mode, tapez la commande suivante :
add BenchmarkTools -
Appuyez sur Entrée et attendez que l’installation se termine.
-
Une fois l’installation terminée, vous pouvez quitter le mode gestionnaire de paquets en appuyant sur la touche Backspace ou Delete.
Alternativement, vous pouvez installer BenchmarkTools directement dans le REPL Julia sans entrer dans le mode gestionnaire de paquets en exécutant :
using Pkg
Pkg.add("BenchmarkTools")Créez et sauvegarder le script suivant
using Plots
using BenchmarkTools
function f(x, y)
return (x - 1)^2 + (y - 2)^2 - 1
end
function solve_equation(x_range, y_range, tolerance)
solutions = Tuple{Float64, Float64}[]
grid_points = Tuple{Float64, Float64}[]
for x in x_range, y in y_range
push!(grid_points, (x, y))
abs(f(x, y)) < tolerance && push!(solutions, (x, y))
end
return solutions, grid_points
end
# Définir les paramètres pour les tests
grid_size = 100
x_range = y_range = range(-10, 10, length=grid_size)
tolerance = 0.01
# Test simple avec @time
println("Performance test using @time:")
@time solve_equation(x_range, y_range, tolerance);
# Test plus précis avec BenchmarkTools
println("\nPerformance test using @benchmark:")
benchmark_result = @benchmark solve_equation($x_range, $y_range, $tolerance)
display(benchmark_result)
# Test de la fonction f séparément
println("\nPerformance test of function f:")
@benchmark f($(x_range[1]), $(y_range[1]))
# Test avec différentes tailles de grille
println("\nPerformance tests with different grid sizes:")
for size in [50, 100, 200, 400]
local x_range = range(-10, 10, length=size)
local y_range = x_range # Utiliser la même plage pour y
println("Grid size: $size x $size")
@time solve_equation(x_range, y_range, tolerance);
endVoici un résumé des caractéristiques principales de ma machine de développement. Composants principaux :
- Processeur : Intel Core i7-13700K
- Carte mère : MSI B760 Gaming Plus WiFi DDR5
- Mémoire : 32 Go DDR5 5200 MHz Kingston FURY Beast (2x16 Go)
- Carte graphique : NVIDIA GeForce RTX 4060 Ti 16 Go GDDR6
- Stockage primaire : SSD NVMe WD BLACK SN850X 2 To
- Stockage secondaire : Aucun disque dur supplémentaire
- Alimentation : Corsair RM850e 850W 80+ Gold
- Boîtier : Systemtreff Plexus-ST-801 (noir) Refroidissement et périphériques :
- Ventirad : Enermax ETS-T50 AXE ARGB (blanc) Système d’exploitation et logiciels :
- Windows 11 Pro 64 bits
Nous obtenons alors les résultats suivants avec cette machine :
Performance test using @time:
0.013812 seconds (12.64 k allocations: 1.248 MiB, 99.57% compilation time)
Performance test using @benchmark:
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 27.600 μs … 6.673 ms ┊ GC (min … max): 0.00% … 98.35%
Time (median): 31.800 μs ┊ GC (median): 0.00%
Time (mean ± σ): 56.762 μs ± 161.322 μs ┊ GC (mean ± σ): 21.97% ± 11.29%
█▅▂▂▂▁▄▄▂ ▁
███████████▇▇▆▅▃▅▅▄▄▆▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄▄▅▆▅▅▅▅▅▅▅▄ █
27.6 μs Histogram: log(frequency) by time 593 μs <
Memory estimate: 652.31 KiB, allocs estimate: 16.
Performance test of function f:
Performance tests with different grid sizes:
Grid size: 50 x 50
0.000019 seconds (15 allocations: 107.469 KiB)
Grid size: 100 x 100
0.000061 seconds (19 allocations: 652.469 KiB)
Grid size: 200 x 200
0.000269 seconds (22 allocations: 1.587 MiB)
Grid size: 400 x 400
0.001010 seconds (27 allocations: 7.982 MiB)
On observe bien évidemment que le temps de calcul augmente avec la taille de la grille mais qu’une majeure partie du temps est passée à la compilation. Nous allons forcer notre fonction de calcul à s’exécuter plus lentement en ajoutant un appel à la fonction sleep.
using Plots
function f(x, y)
sleep(1E-9)
return (x - 1)^2 + (y - 2)^2 - 1
end
function solve_equation(x_range, y_range, tolerance)
solutions = Tuple{Float64,Float64}[]
grid_points = Tuple{Float64,Float64}[]
for x in x_range, y in y_range
push!(grid_points, (x, y))
abs(f(x, y)) < tolerance && push!(solutions, (x, y))
end
return solutions, grid_points
end
# Définir les paramètres pour les tests
grid_size = 100
x_range = y_range = range(-10, 10, length=grid_size)
tolerance = 0.01
# Test simple avec @time
println("Performance test using @time:")
@time solve_equation(x_range, y_range, tolerance);L’exécution de ce script indique désormais un temps d’exécution d’environ 2 minutes 35.
Performance test using @time:
155.584363 seconds (64.85 k allocations: 3.034 MiB, 0.01% compilation time)
C’est assez long… et pénible d’attendre… diminuons la taille de la grille à 10 x 10.
Performance test using @time:
1.560340 seconds (24.26 k allocations: 1.203 MiB, 0.99% compilation time)
Le temps de calcul se réduit d’un facteur 100. Voyons maintenant l’influence du multithreading.